Finansal Piyasalara Fraktal Yaklaşım – Benoit Mandelbrot

Benoit Mandelbrot, hemen her alanda geleneksel düşünce tarzımızı sarsan ve “fraktal” kavramıyla bize bambaşka dünyalar açan matematikçi, bilimdadamı ve filozof. En önemli eseri mandelbrot kümesi diye adlandırılan sanal karmaşık sayıların görselleştirilmesiyle oluşturulan ve kendini sonsuz kez tekrarlayıp sonsuz şekiller üreten kümedir.

Mandelbrot’un dünyasına girmeden önce Nassim Nicholas Taleb yazılarımı okumanızı öneririm. Nassim Nicholas Taleb Mandelbrot’un öğrencisidir ve öğretilerini kullanarak literatüre altın harflerle kazınacak Siyah Kuğu kitabını yazmıştır. Benoit Mandelbrot’u ve fikirlerini anlatan Finans Piyasalarında (Saklı) Düzen kitabının notlarını aşağıda paylaşıyorum.

• “Gelenekçi finans teorisi fiyatlardaki yukarı ve aşağı değişimlerin yazı tura atmayla belirlendiği, en basit anlamıyla “sakin” hale uyan rastgele süreçlerle modellenebileceğini kabul eder. Halbuki fraktallar dolayısıyla fiyatların bu modele çok uyumsuz olduğu görülmektedir. Vahşi fiyat hareketlerini daha doğru gösterebilecek multifraktal bir model bizi daha güvenilir bir finans teorisine götürecektir.”

Burada kastedilen sizin de tahmin edeceğiniz üzere Brownian Motion ve Gaussian Distribution. Bu tarz yöntemler kullanıldığında milyonda bir olasılıkla gerçekleşecek olayların bile çok sık gerçekleştiğini rahatlıkla görebiliyoruz.

Günümüzde yaygın olarak kullanılan normal dağılımın gerçeği karşılamadığını ve fiyatların çok daha fazla değişebildiğini ve fiyat dağılımlarının “fat tail” e sahip olduğunu göstermiştir.

• “Fiyatlar sürekli bir hareketten ziyade sıçrayarak değişir. Bugünkü fiyat değişimleri çok eski fiyat değişimlerine bağlı olablir.”
• “Eğer Mandelbrot haklıysa en küçük kareler yöntemi, spektral analiz, maksimum olası çözümler, örnekleme teorisi, kapalı dağılımlar gibi istatistiksel yöntemlerin neredeyse hepsi kullanılamaz hale gelecektir.
• “Matematiğin bu yeni dalındaki asıl katkım, görünüşte düzensiz olan bir sistemde düzenin, plansız olanda bir planın, düzensiz ve pürüzlü olanda belirli bir yapı olduğunu göstermek oldu. Fraktal geometri olarak adlandırılan bu dal, hava tahmin modellerinde, ırmakların akışında, beyin dalgalarının analizinde, sismik sarsıntılarda ve galaksilerin dağılımının anlaşılması gibi bir çok alanda kullanıldı.
• “Hisse senedi fiyatları önceden bilinemez ama risk matematiksel olarak ifade edilip bilgisayarda modellenebilen belirli bir yapıyı takip eder.”
• “Fiyat değişimleri birbirinden bağımsız değildir. Son birkaç on yılda yapılan çalışmalarda çoğu fiyat serisinin belleğe sahip olduğu gösterilmiştir. Bugünün olayı yarını da etkiler. Eğer fiyatlar bugün büyük oranda değişiyorsa, ertesi gün de böyle hareket etme olasılığı yüksek olur.”
• “Benim aykırı düşüncem ise uzun vadeli belleğe sahip fraktal bir istatistiksel ilişkidir.”
• “Gerçekte veriler çan eğrisine çok az uyarlar.”
• “Piyasalardaki türbülans kümelenme eğilimi gösterir. Seans odalarında her işlem sabahının ilk on beş dakikasının kritik öneme sahip olduğu dünyanın her yerinde bilinir.”
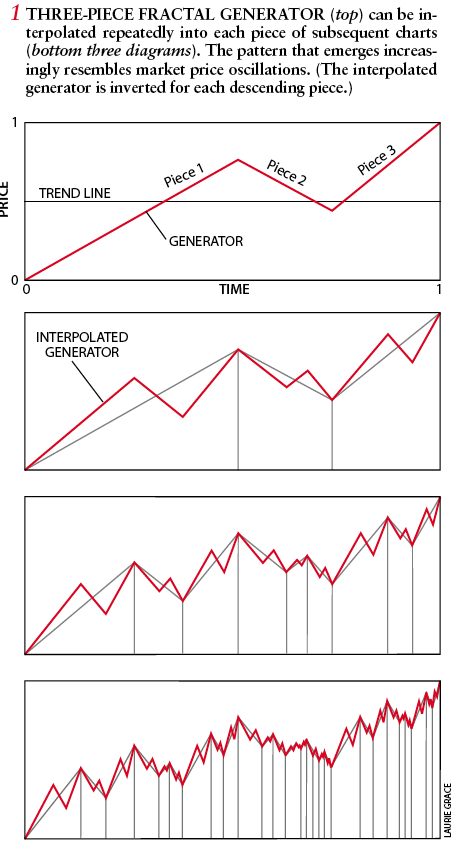
• Fraktal modellemede temel unsur çok basit bir rastgele olayda bile oldukça karmaşık bir yapı ortaya çıkabilmesidir.

• Borsadaki hareketleri belirleyen faktörlerin sayısı çok fazladır ve genellikle fiyatlarla doğrudan ilişkilendirilmeyen, gerçekleşmekte olan veya beklenen olaylarla doludur. Borsa kendi kendisine tepki verebilir ve gerçekleşmekte olan işlemler yalnızca geçmişin bir fonksiyonu değil, aynı zamanda piyasanın geri kalanıyla olan ilişkilerine de bağlıdır. Bu etkinliğin belirlenmesi sonsuz sayıdaki faktöre bağlıdır. Bu yüzden matematiksel bir tahmin yürütmek olanaksız görülür. Ama piyasanın belirli bir andaki durumu, yani piyasanın o anda bulunduğu duruma göre oluşacak fiyat hareketlerinin olasılığını veren matematiksel bir inceleme yapmak mümkündür. Piyasa dalgalanmaları tahmin edilemez olsa da hangi hareketin daha yüksek ve daha düşük bir olasılıkla gerçekleşeceği matematiksel olarak hesaplanabilir. (Theorie de la Speculation)
• “Finans dünyasında kabul görmüş en popüler ama en anlamsız 4 teori şöyledir:
  • İnsanlar mantıklıdır ve zengin olmayı hedeflerler.
  • Bütün yatırımcılar birbirine benzer
  • Fiyat değişimi pratikte süreklidir
  • Fiyat değişimleri Brown hareketine uyar
    • Fiyat hareketleri bağımsızdır
    • Fiyat değişimleri istatistiksel olarak durağandır
    • Fiyat normal dağılıma uyar.”
• “Bağımlılığın en önemli etkileri kısa vadede değil, çok uzun vadede, teoride sonsuzdadır.”
• “Fraktal, her bir parçanın bütünün yansıması olduğu desen veya şekillerdir. Fraktal geometri gücünü çok sayıda karmaşık ve düzensiz veriyi birkaç basit formülle ifade edebilmesinden alır. Başlangıçta kullanılan şablon sonuç olarak çıkan şekli etkilediği için bağımlılık söz konusudur.”

• “Bir fraktal bütünü parçalarıyla ilişkilendiren özel bir tür değişmezliğe sahiptir. Bütün, her biri kendisini aksettiren daha küçük parçalara ayrılabilir.”
• “Ekonomi gazeteleri çünkülerin üzerine atlar ve onları önem sırasına göre dizerek haberleri satarlar. Makraekonomik ve sektörel alanlarda sınıflanmış binlerce temel analizciyi bünyelerinde çalıştırırlar. Piyasa düzenleyicileri kuralları belirler ve bir şirketin yatırımcılarına ne anlatması gerektiğini dikte ettirir. Bunun ardında yatan ise, bir olayın nedeni bilindiği takdirde geleceğin tahmin edilebileceği ve riskin yönetilebileceği kabulüdür
• “Fraktallardaki temel mantık basit kurallar karmaşık yapılar meydana getirir ve karmaşık yapılar basit kurallara indirgenebilir.”
• “Demokrasi bir aldatmacadır. İnsan doğası ilkel, duygusal ve boyun eğmezdir. Daha zeki, güçlü, yetenekli ve açıkgöz olanlar aslan payını alır.”
• “Haberleri fiyata, nedeni etkiye bağlayan piyasa mekanizması gizemli ve tutarsız görünür. Savaş tehlikesi belirir, dolar düşer, savaş tehlikesi belirir, dolar yükselir. Bu ikisinden hangisi gerçekte olacaktır. Ancak olay gerçekleştikten sonra temel analiz kullanılabilir ve iyi sonuç verir. Ama gerçekleşmeden önce her iki seçenek de aynı olasılığa sahip gibi görünür.”
• “Fiyat hareketleri incelenirken yüzde değişim frekansı ve yüzde değişimlerin logaritması alınarak (log-log) inceleme yapılabilir. Pareto dağılımı göz önünde bulundurulmalıdır.
• “Uzun vadeli bellek sayesinde geçmiş bugünün rastgele dalgalanmalarını etkilemeye devam eder.”
• “Enflasyon inatçıdır, eğrisi oldukça yavaş azalır. Enflasyon bir kez başladı mı onu yavaşlatmak zordur.”
• “Çan eğrisinin fiyat hareketleri doğru verdiği farz edilirse, Markowitz’in öne sürdüğü gibi varyans ve standart sapma risk için uygun seçilmiş parametrelerdir. Markowitz’in haklı olması durumunda, Sharpe’ın beta ve sermaye bedeli tahmini anlamlı olur. Çan eğrisinin kabülü ve fiyat hareketlerinin sürekli olma kabulü altında Black – Scholes formülü doğrudur. Ama zincir en zayıf halkası kadar sağlamdır.”
• “Orjinal Brown hareketinde, bir molekül iki nano saniye sonra ne kadar uzağa gider. Karekök kuralı geçerlidir. 100 saniye hareket eden bir Brown parçacığı 1 saniye hareket edene göre 10 kat daha fazla yol alır. Peki tahminler yapılırken karekökten farklı bir değer alırsa ne olur? Bu değer 0 ile 1 arasında değişebilir. 1 e yaklaştıkça trendli bir hareket yaparken, 0 a yaklaştıkça daha az dolaşır ve her adım bir öncekinin tersi yönünde olmaya eğilimlidir.”
• “Oynaklık farklı yerlerde kümelenir. Büyük fiyat değişimleri birbirinden durgun bölümlerle ayrılan kümelerde toplanırlar.”
• “Bir gün önce fiyatların düşmüş olması bugün de düşmelerini daha olası yapmaz. Mutlak farkların bağımlı olmaları mümkündür. Bir gün önceki %10’luk düşüş, bugün de %10luk bir hareketin olma olasılığını arttırır, ama önceden bunun yukarı mı yoksa aşağı yönde mi olacağı hakkında bir öngörüde bulunamayız.”